Page 70 - MECÁNICA PARA INGENIERÍA Y SUS APLICACIONES – DINÁMICA Capítulo III

MECÁNICA PARA INGENIERÍA Y SUS APLICACIONES – DINÁMICA Capítulo III


3
M  3   M 2


H        i    sen  j   i    sen  j (0)
0
 3  8 8  12
Derivando (0), con respecto al tiempo en el marco inercial () y usando la ecuación “I”:

0
    
    x H  M 2  cos j    x H (1)
H 
H 

0
0
 0 12   0
i j k
M 2



  x H   sen   cos
0
 12


 sen  0
M 2

 
 x H    sen cos     cos   j (2)

i

 0 12

(2) en (1):

   M 2  sen cos i    2  cos  j
 

H
0
12
 

 M  H  M  2   cos (Unidades de momento)
y
0
y
6

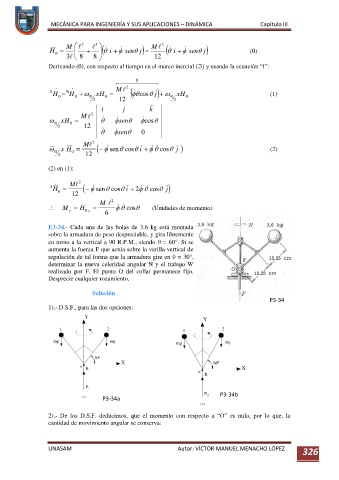
E3-34.- Cada una de las bolas de 3.6 kg está montada
sobre la armadura de peso despreciable, y gira libremente
en torno a la vertical a 90 R.P.M., siendo  = 60°. Si se
aumenta la fuerza F que actúa sobre la varilla vertical de
regulación de tal forma que la armadura gire en  = 30°,
determinar la nueva celeridad angular N y el trabajo W
realizado por F. El punto O del collar permanece fijo.
Desprecie cualquier rozamiento.

Solución
P3-34
1).- D.S.F., para las dos opciones:
Y
Y
1 2 1 2

mg mg mg mg

30º
o X 60º X
R o R

F 1
( 1 ) F 2 P3-34b
P3-34a ( 2 )

2).- De los D.S.F. deducimos, que el momento con respecto a “O” es nulo, por lo que, la
cantidad de movimiento angular se conserva:

UNASAM Autor: VÍCTOR MANUEL MENACHO LÓPEZ 326