Page 108 - MECÁNICA PARA INGENIERÍA Y SUS APLICACIONES – DINÁMICA Capítulo III

MECÁNICA PARA INGENIERÍA Y SUS APLICACIONES – DINÁMICA Capítulo III

T  21.42 N

En (2):
T  38.86 N
2
3).- Relaciones cinemáticas.

Con a  3.79 m/s , se calcula la altura h:
2
1 5.79*4
2
h  a t   11.58m
2 2
II).- Por el método energético en el sistema de partículas. La energía potencial de caída se
convierte en cinética de los tres bloques y perdida por fricción.

a).- Relaciones cinéticas, para el sistema eliminando las fuerzas internas de (1), (2) y (3),
sumándoles:
 F ext   m a i  15g  5 sen30  0.4*5 cos30  0.4*4 g  5a  4a  15a
0
0
g
g
i
138.98 24a  a  5.79 m/s

2
Como: v  a t  5.79*2 11.58 m/s

b).- Por balance el método alternativo del principio de trabajo y energía:

1
0
0
15 *h  5 * sen30  5 4 15 v   2  0.4*4 *h  0.4*5 * cos30
g
h
g
g
h
g
2
h *g 15 2.5 0.4*4 0.4*5cos30   0  12*11.58 2
138.99h  1609.16  h  11.5775 11.58 m

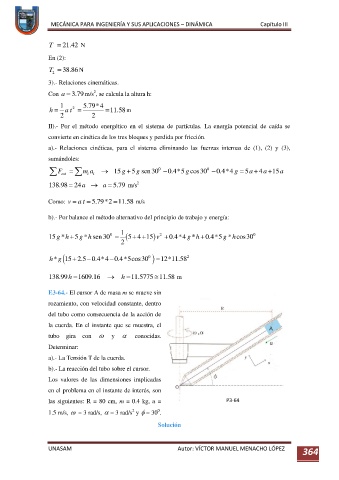
E3-64.- El cursor A de masa m se mueve sin
rozamiento, con velocidad constante, dentro
del tubo como consecuencia de la acción de
la cuerda. En el instante que se muestra, el

tubo gira con  y  conocidas.
Determinar:

a).- La Tensión T de la cuerda.
b).- La reacción del tubo sobre el cursor.
Los valores de las dimensiones implicadas

en el problema en el instante de interés, son
las siguientes: R = 80 cm, m = 0.4 kg, u = P3-64

0
2
1.5 m/s,  = 3 rad/s,  = 3 rad/s y  = 30 .
Solución

UNASAM Autor: VÍCTOR MANUEL MENACHO LÓPEZ 364