Page 115 - MECÁNICA PARA INGENIERÍA Y SUS APLICACIONES – DINÁMICA Capítulo III

MECÁNICA PARA INGENIERÍA Y SUS APLICACIONES – DINÁMICA Capítulo III

 F  ma Cy  N mg cos  m    2b  2v 

y
 2 
N  m   g    2b   2v    (Unidades de Fuerza)
2
2
 2 

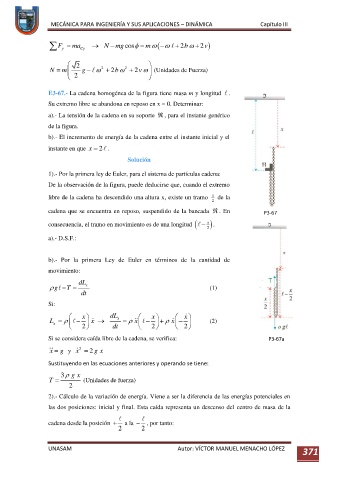
E3-67.- La cadena homogénea de la figura tiene masa m y longitud .
Su extremo libre se abandona en reposo en x = 0. Determinar:
a).- La tensión de la cadena en su soporte  , para el instante genérico

de la figura.
b).- El incremento de energía de la cadena entre el instante inicial y el

instante en que x  2 .
Solución

1).- Por la primera ley de Euler, para el sistema de partículas cadena:

De la observación de la figura, puede deducirse que, cuando el extremo
x
libre de la cadena ha descendido una altura x, existe un tramo de la
2
cadena que se encuentra en reposo, suspendido de la bancada  . En P3-67
consecuencia, el tramo en movimiento es de una longitud   x  .
2
a).- D.S.F.:

b).- Por la primera Ley de Euler en términos de la cantidad de
movimiento:

dL
 g  T  x (1)
dt

Si:

L     x  x  dL x   x   x    x  x  (2)






x
 2  dt  2   2 
Si se considera caída libre de la cadena, se verifica: P3-67a
x  g y x  2 g x
2
Sustituyendo en las ecuaciones anteriores y operando se tiene:
3 g x
T  (Unidades de fuerza)
2
2).- Cálculo de la variación de energía. Viene a ser la diferencia de las energías potenciales en
las dos posiciones: inicial y final. Esta caída representa un descenso del centro de masa de la

cadena desde la posición  a la  , por tanto:
2 2

UNASAM Autor: VÍCTOR MANUEL MENACHO LÓPEZ 371